Loading... 机器学习_分类_SVM <!--more--> ### 支持向量机 (Support Vector Machine, SVM)的基本模型是在特征空间上找到最佳的 `分离超平面`使得训练集上正负样本间隔最大。 二分类问题的有监督学习算法,引入了核方法之后SVM也可以用来解决非线性问题 一般SVM有下面三种: > 1、硬间隔支持向量机(线性可分支持向量机):当训练数据线性可分时,可通过硬间隔最大化学得一个线性可分支持向量机。<br> 2. 软间隔支持向量机:当训练数据近似线性可分时,可通过软间隔最大化学得一个线性支持向量机。<br> 3. 非线性支持向量机:当训练数据线性不可分时,可通过核方法以及软间隔最大化学得一个非线性支持向量机。 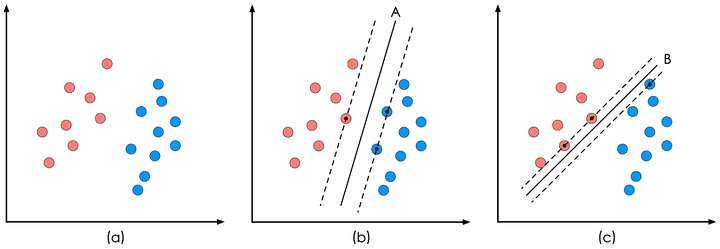 SVM算法认为图1中的分类器A在性能上优于分类器B,其依据是A的分类间隔比B要大 > 这两条平行虚线正中间的分界线就是在保持当前决策面方向不变的前提下的最优决策面。两条虚线之间的垂直距离就是这个最优决策面对应的 `分类间隔`。<br> > 那个具有“最大间隔”的决策面就是SVM要寻找的最优解,而这个真正的最优解对应的两侧虚线所穿过的样本点,就是SVM中的支持样本点,称为 `支持向量`。<br> > 对于图1中的数据,A决策面就是SVM寻找的最优解,而相应的三个位于虚线上的样本点在坐标系中对应的向量就叫做 `支持向量`。 ### 基于最大间隔分割数据 优点,错误率低,计算开销不大,结果容易解释 缺点,对参数调节敏感,原始分类器不加修改只能解决二类问题。 $ w^{t}x+b $为分类函数<br> 输人数据给分类器会输出一个类别标签,单位阶跃函数)的函数对$$ w^{t}x+b $$作用得到$$ f(w^{t}x+b) $$,其中当u<0时输出-1, 反之则输出+1。这是由于-1和+1仅仅相差一个符号,方便数学上的处理。 如果数据点处于正方向(即+1类 )并且离**分隔超平面**很远的位置时,$$ w^{t}x+b $$会是一个很大的正数,同时$$ label*(w^{t}x+b) $$也会是一个很大的正数。而如果数据点处于负方向(-1类 )并且离**分隔超平面**远的位置时,此时由于类别标签为-1,则$$ label*(w^{t}x+b) $$仍然是一个很大的正数。 目标:找到分类器定义中的w和b。找到具有最小间隔的数据点即**支持向量**。找到支持向量,对间隔最大化。  SVM的目标函数:  分离超平面分类函数为0,支持向量的分类函数为+-1,为了优化目标函数,固定一个优化另外一个,该问题是一个带约束条件的优化问题。这里的约束条件就是$$ label*(w^{t}x+b)=1 $$。<br> 注:$$ label*(w^{t}x+b) $$被称为点到分隔面的函数间隔,$$ label*(w^{t}x+b)*(1/w) $$称为点到分隔面的几何间隔。<br> 求解这个问题需要经过一系列的转换。具体如下:  求$ 1/W$的最大值相当于求$0.5w^2$的最小值,一个凸二次规划问题  ``` 注:新目标函数约束条件: alpha>=0,所有的aplha*lable=0 但是数据未必100%线性可分,引人所谓松弛变量C 新目标函数约束条件为: C>alpha>=0,所有的aplha*lable=0 ``` SVM中的主要工作就是求解这些alpha。<br> SMO算法(序列最小优 化(SequentialMinimalOptimization ))<br>的目标是求出一系列alpha和b,一旦求出了这些alpha,就很容易计算出权重向量w,并得到分隔超平面。 >SMO的工作原理是:每次循环中选择两个alpha进行优化处理,一旦找到一对合适的alpha,那么就增大其中一个,同时减小另一个。选择的alpha要满足在间隔边界之外的条件,而且还没有进行过区间化处理或者不再边界上。 ### 核函数: 大部分时候数据并不是线性可分的,这个时候满足这样条件的超平面就根本不存在。在上文中,我们已经了解到了SVM处理线性可分的情况,那对于非线性的数据SVM咋处理呢?对于非线性的情况,SVM 的处理方法是选择一个核函数,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。 这是原始数据和原始空间,明显有红蓝两类:  通过核函数,将样本数据映射到更高维的空间(在这里,是二维映射到三维):  而后进行分离超平面:  再将分割的超平面映射回去:  效果图:  >核函数的选择变成了支持向量机的最大变数(如果必须得用上核函数,即核化),因此选用什么样的核函数会影响最后的结果。而最常用的核函数有:线性核、多项式核、高斯核、拉普拉斯核、sigmoid核、通过核函数之间的线性组合或直积等运算得出的新核函数。 Opencv代码: ``` #include <opencv2/core/core.hpp> #include <opencv2/highgui/highgui.hpp> #include <opencv2/ml/ml.hpp> using namespace cv; int main() { // Data for visual representation int width = 512, height = 512; Mat image = Mat::zeros(height, width, CV_8UC3); // Set up training data float labels[5] = {1.0, -1.0, -1.0, -1.0,1.0}; Mat labelsMat(5, 1, CV_32FC1, labels); float trainingData[5][2] = { {501, 10}, {255, 10}, {501, 255}, {10, 501},{501,128} }; Mat trainingDataMat(5, 2, CV_32FC1, trainingData); //设置支持向量机的参数 CvSVMParams params; params.svm_type = CvSVM::C_SVC;//SVM类型:使用C支持向量机 params.kernel_type = CvSVM::LINEAR;//核函数类型:线性 params.term_crit = cvTermCriteria(CV_TERMCRIT_ITER, 100, 1e-6);//终止准则函数:当迭代次数达到最大值时终止 //训练SVM //建立一个SVM类的实例 CvSVM SVM; //训练模型,参数为:输入数据、响应、XX、XX、参数(前面设置过) SVM.train(trainingDataMat, labelsMat, Mat(), Mat(), params); Vec3b green(0,255,0), blue (255,0,0); //显示判决域 for (int i = 0; i < image.rows; ++i) for (int j = 0; j < image.cols; ++j) { Mat sampleMat = (Mat_<float>(1,2) << i,j); //predict是用来预测的,参数为:样本、返回值类型(如果值为ture而且是一个2类问题则返回判决函数值,否则返回类标签)、 float response = SVM.predict(sampleMat); if (response == 1) image.at<Vec3b>(j, i) = green; else if (response == -1) image.at<Vec3b>(j, i) = blue; } //画出训练数据 int thickness = -1; int lineType = 8; circle( image, Point(501, 10), 5, Scalar( 0, 0, 0), thickness, lineType);//画圆 circle( image, Point(255, 10), 5, Scalar(255, 255, 255), thickness, lineType); circle( image, Point(501, 255), 5, Scalar(255, 255, 255), thickness, lineType); circle( image, Point( 10, 501), 5, Scalar(255, 255, 255), thickness, lineType); circle(image, Point( 501, 128), 5, Scalar(0, 0, 0), thickness, lineType); //显示支持向量 thickness = 2; lineType = 8; //获取支持向量的个数 int c = SVM.get_support_vector_count(); for (int i = 0; i < c; ++i) { //获取第i个支持向量 const float* v = SVM.get_support_vector(i); //支持向量用到的样本点,用灰色进行标注 circle( image, Point( (int) v[0], (int) v[1]), 6, Scalar(128, 128, 128), thickness, lineType); } imwrite("result.png", image); // save the image imshow("SVM Simple Example", image); // show it to the user waitKey(0); } ``` $$ 最后修改:2020 年 08 月 08 日 © 允许规范转载 打赏 赞赏作者 支付宝微信 赞 如果觉得我的文章对你有用,请随意赞赏